Ответы к экзамену по дисциплине "Информатика" (Часть 1)
[
· Скачать (295.98 Kb)
]
 Ответы к экзамену по дисциплине "Информатика" (Часть 1)
Ответы к экзамену по дисциплине "Информатика" (Часть 1)2. Применение метода конечных разностей при определении прогиба нерастяжимой мембраны под действием распределенной нагрузки на ее поверхности и распределенных растягивающих усилий по периметру.
3. Применение метода конечных разностей при решении одномерной задачи теплопроводности стены и заданных начальных и краевых условиях.
4. Применение метода Эйлера при определении прогиба консоли под действием распределенной нагрузки и сосредоточенной силы.
5. Элементы теории задачи линейного программирования при производстве двух видов бетона в зависимости от расхода цемента, песка и щебня.
6. Алгоритмы численного решения нелинейных и трансцендентных уравнений.
7. Алгоритмы решение нелинейных и трансцендентных уравнений методом половинного деления. Критерии точности и условия сходимости решения.
8. Алгоритмы решения нелинейных и трансцендентных уравнений методом итерации. Критерии точности и условия сходимости решения.
9. Алгоритмы решения нелинейных и трансцендентных уравнений методом Ньютона. Критерии точности и условия сходимости решения.
10. Сравнительный анализ и применение в инженерных расчетах методов численного решения систем линейных алгебраических уравнений.
11. Алгоритмы решения систем линейных алгебраических уравнений методом Гаусса. Критерии точности и условия сходимости решения.
12. Алгоритмы решения систем линейных алгебраических уравнений методом простой итерации. Критерии точности и условия сходимости решения.
13. Алгоритмы решения систем линейных алгебраических уравнений методом Зейделя. Критерии точности и условия сходимости решения.
14. Алгоритмы вычисления собственных значений и векторов матриц и их применение в инженерных расчетах.
15. Сравнительный анализ и применение в инженерных расчетах методов численного интегрирования функций.
16. Сравнительный анализ текущей погрешности и скорости численного интегрирования функций методом прямоугольников и методом трапеций.
17. Сравнительный анализ текущей погрешности и скорости численного интегрирования функций методом Симпсона и методом трапеций.
18. Применение численного дифференцирования функций в инженерных расчетах.
19. Алгоритмы численного дифференцирования функций с разложением в ряд Тейлора.
20. Левостороннее и правостороннее приближение производной при численном дифференцировании функций.
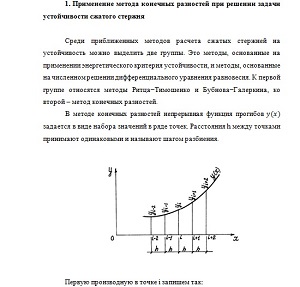
21. Применение метода конечных разностей при решении дифференциальных уравнений.
22. Алгоритмы численного решения обыкновенного дифференциального уравнения первого порядка методом Эйлера с начальными условиями (Задача Коши).
23. Применение метода Эйлера для определения функции угла отклонения математического маятника от положения равновесия в режиме свободных колебаний.
24. Решения задач линейного программирования по повышению рентабельности и доходности строительного производства.
Год: 2014
Страниц: 41
Формат: Word
· Скачать Ответы к экзамену по дисциплине "Информатика" (Часть 1) (295.98 Kb)